Ich habe Tom Fiddamans systemdynamisches COVID-19-Modell, das er für Bozeman (Montana) kalibriert hat, an die Verhältnisse im Kreis Bergstraße (meinem Wohnort) angepasst — disaggregiertere System-Dynamics-Modelle haben beispielsweise Jeroen Struben, Kim Warren oder iSee-Systems entwickelt (und hier das Video des Outputs eines agenten-basierten Modells einer Infektion und noch ein Artikel der Washington Post mit einer eingebetteten Agentensimulation). Die wesentlichen Annahmen des Modells erklärt Tom im Video auf obiger Webseite; geändert habe ich nur die Anzahl Bewohner, Intensivbetten, Auftreten der ersten Infektion, und die Basisreproduktionszahl (R0), die wohl etwas kleiner als im Originalmodell angegeben liegen dürfte. Hier ein Screenshot des System-Dynamics-Modells (grundsätzliche Informationen zu COVID-19 hier und hier; eine einfach Diskussion unterschiedlicher Infektionen in einem früheren Beitrag):
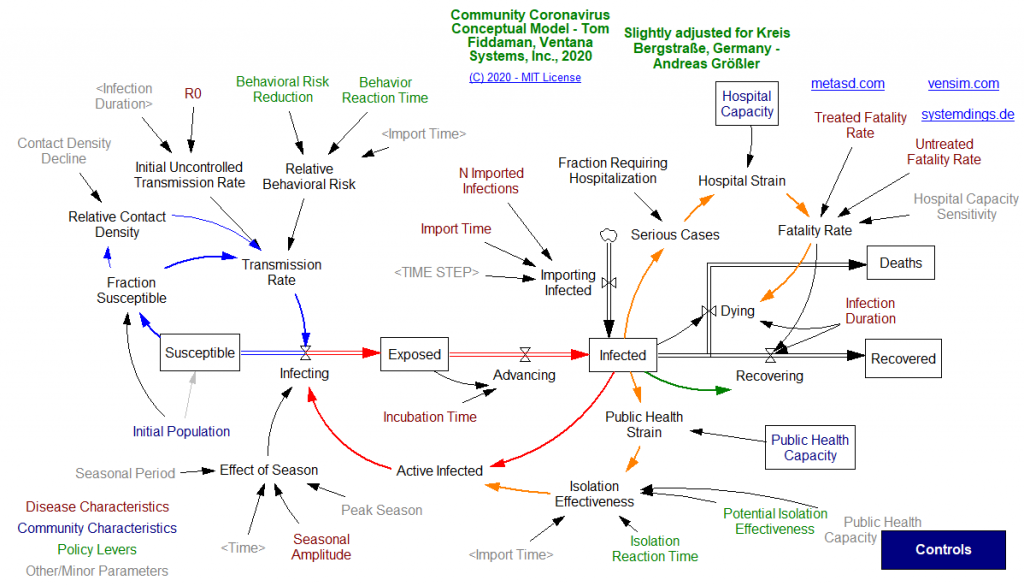
Achtung: das Modell dient nicht zur genauen Vorhersage möglicher Fallzahlen; aber es erlaubt, die grundsätzlichen Auswirkungen einzelner Variablen oder Policies zu testen, da das Systemverhalten (hier bspw. Verlauf der Infektion) von der Systemstruktur (hier: Infektionsmodell) abhängt. Ein Modell zur genaueren Vorhersage und politischen Entscheidungsunterstützung sollte wesentlich disaggregierter sein und einige der zusätzlichen Annahmen auflösen — so könnte z.B. die Auswirkung ganz konkreter Verhaltensänderungen erfasst und abgetestet werden; oder in gefährdete (ältere, vorerkrankte) und ungefährdete Infizierte unterschieden werden. Hier also die Simulationsergebnisse für nur prototypische Szenarien (nochmals: keine Panik und mit Vorsicht genießen, aber daraus lernen):
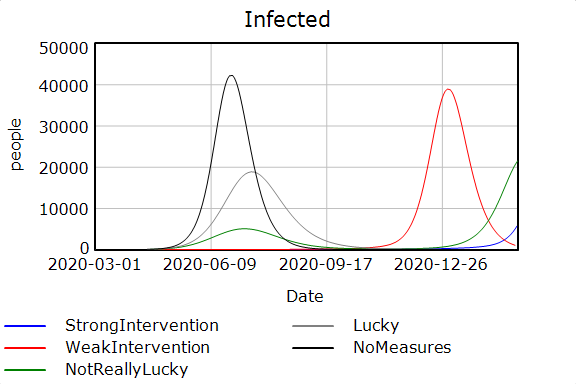
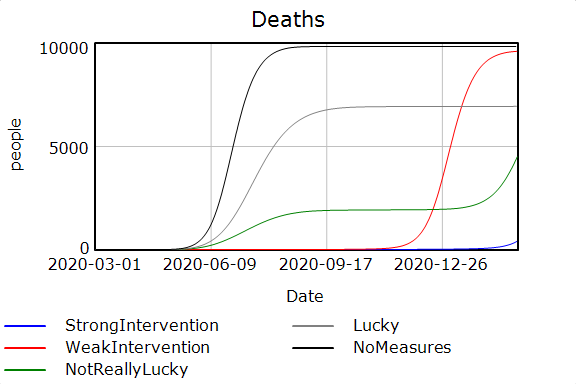
Das Szenario „NoMeasures“ ist ein kontrafaktisches Worst-Case-Szenario, da es davon ausgeht, dass keinerlei Interventionen vorgenommen werden, also insbesondere keine Quarantäne für Infizierte und keine Verhaltensänderung (Hygienemaßnahmen, Vermeidung von sozialen Kontakten) in der Bevölkerung und auch die Infektionscharakteristika sehr unvorteilhaft sind. Die Todeszahlen zeigen, dass die Auswirkungen katastrophal wären.
Das Szenario „Lucky“ ist evtl. etwas falsch benannt; hier wurde Saisonalität der Epidemie unterstellt, was zu einem Rückgang der Infektionen im Sommer führen würde–bis dahin kommt es aber auch zu sehr vielen Toten. Das Szenario „NotReallyLucky“ nimmt eine noch stärkere Saisonalität an: zwar werden dann in diesem Jahr noch weniger Menschen infiziert und sterben; allerdings tritt dann im nächsten Jahr wieder eine Infektionswelle auf, der wiederum vielen Menschen zum Opfer fallen würden.
In den Szenarien „WeakIntervention“ und „StrongIntervention“ wird davon ausgegangen, dass die Hälfte der Infizierten rechtzeitig in Quarantäne kommt. Die Unterschiede ergeben sich hier allein durch die Verhaltensanpassung in der Bevölkerung: sind diese nur halbherzig, kommt es lediglich zu einem zeitlichen Verschieben der Infektionswelle auf später; nur wenn die Verhaltensänderungen stark genug ausfallen, kann die Infektion nicht um sich greifen (der blaue Graph ist aufgrund der Skalierung in den Abbildungen kaum zu sehen und bis zum Ende des Betrachtungszeitraums im Wesentlichen parallel zur x-Achse). Am Ende des Simulationszeitraums von einem Jahr kommt es aber auch dann zu einem Ansteigen der Infizierten bzw. der Todeszahlen — allerdings ist zu hoffen, dass bis dahin ein Impfstoff vorhanden ist.
Im Weiteren interessant wären natürlich auch Kombinationen verschiedener Szenarien. Eine Botschaft wird allerdings klar: es müssen deutliche Verhaltensanpassungen stattfinden, um nicht in eine Gesundheitskatastrophe zu geraten. Denn auch falls die Zahlen in dieser Simulation um das Hundertfache überschätzt wären, ergäben sich ohne Interventionen noch signifikante Todeszahlen, die wir nicht als unabdingbar hinnehmen sollten.